Mit der Elbow-Methode kannst du herausfinden, wie viele unterschiedliche Cluster sich für dein Dataset am besten eignen. Wenn du das weisst, kannst du mit dem k-means-Cluster-Algorithmus bestimmen, bei welchen Werten die Schwellenwerte für diese Cluster liegen.
Das ist unser Test Data Set:
| Auftragsnr | Artikel_ID | Monat | Umsatz | Auftragsmenge | Retourenmenge | Artikelbeschreibung | Lieferanten_ID | Lieferantenbeschreibung | Warengruppe | Marke |
|---|---|---|---|---|---|---|---|---|---|---|
| 1093 | 90 | February | 366.23 | 2 | 1 | Artikel 90 | 1 | Lieferant 10 | Elektronik | Marke 11 |
| 1047 | 81 | July | 381.17 | 2 | 1 | Artikel 81 | 8 | Lieferant 8 | Haushalt | Marke 11 |
| 1009 | 87 | August | 203.08 | 4 | 0 | Artikel 87 | 10 | Lieferant 6 | Haushalt | Marke 6 |
| 1024 | 53 | March | 158.24 | 5 | 1 | Artikel 53 | 6 | Lieferant 10 | Elektronik | Marke 16 |
| 1037 | 10 | February | 275.21 | 2 | 3 | Artikel 10 | 10 | Lieferant 3 | Spielzeug | Marke 2 |
| 1099 | 41 | June | 144.63 | 3 | 0 | Artikel 41 | 2 | Lieferant 5 | Spielzeug | Marke 12 |
Die Elbow-Methode einfach erklärt
Die Elbow-Methode basiert auf der Variation: Je gleichmässiger die Variation bei einer bestimmten Anzahl von Clustern ist, desto wahrscheinlicher ist es, dass diese Clusteranzahl die richtige Wahl ist.
Um das zu veranschaulichen, habe ich die Datenpunkte auf eine Linie gesetzt, alle in einem einzigen Cluster zusammengefasst und dann die Variation berechnet. Natürlich ist die Variation bei nur einem Cluster nicht besonders aufregend, wie man im Bild sieht.
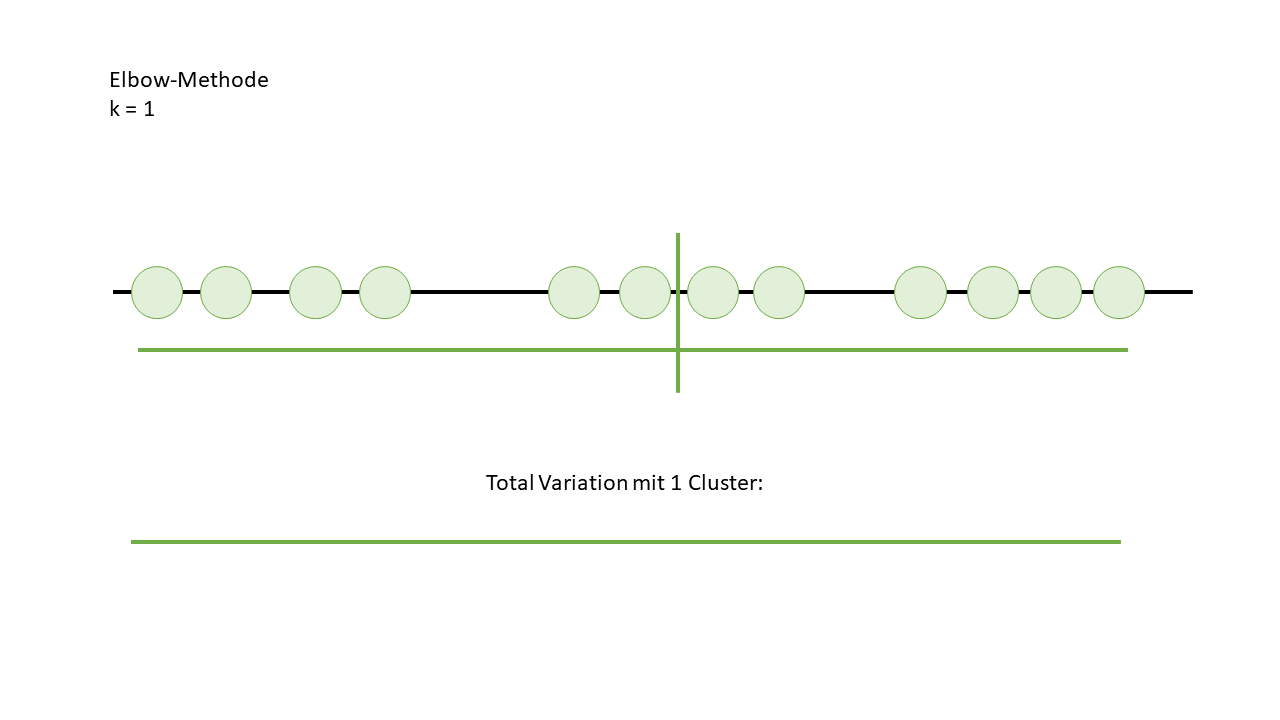
Um die richtige Anzahl von Clustern zu finden, muss dieser Prozess natürlich mit verschiedenen Clusteranzahlen wiederholt werden. Dabei wird die Variation für jede Clusteranzahl berechnet, und die Ergebnisse werden dann miteinander verglichen. Ziel ist es, den Punkt zu finden, an dem eine weitere Erhöhung der Clusteranzahl zu einer deutlich geringeren Gleichmässigkeit der Variation führt – das ist der sogenannte "Elbow-Punkt", der auf die optimale Clusteranzahl hinweist.
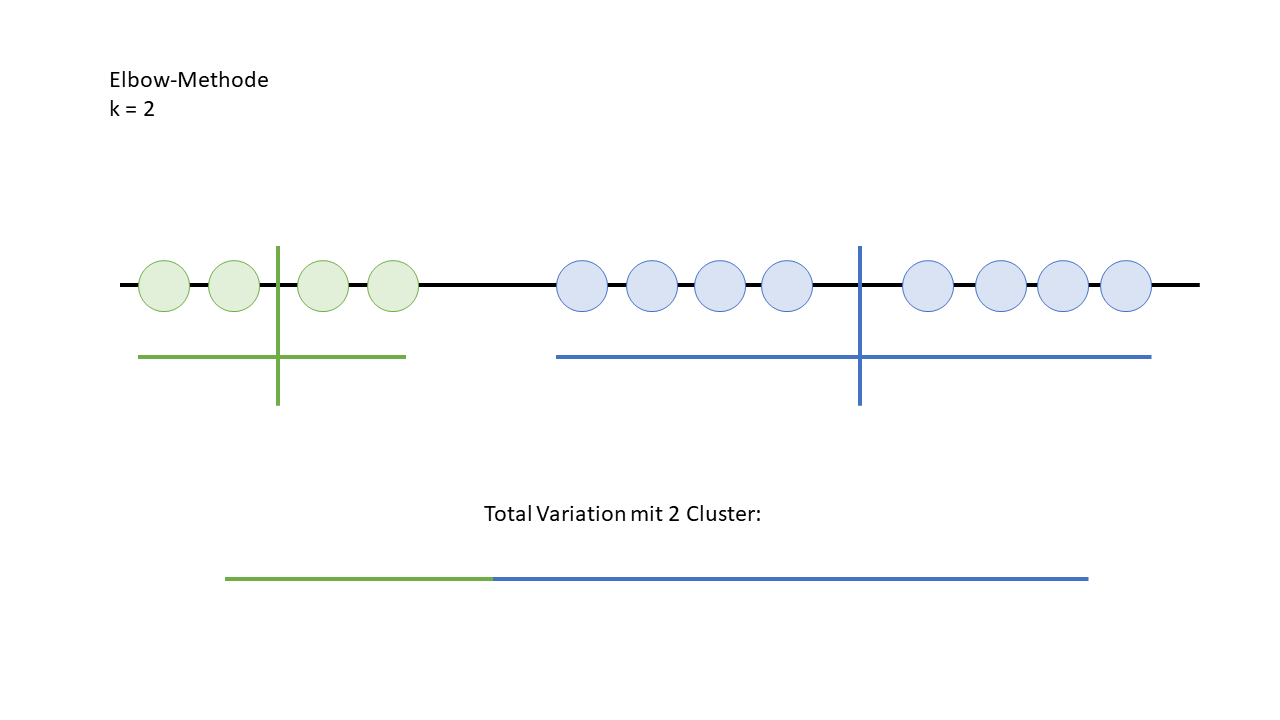
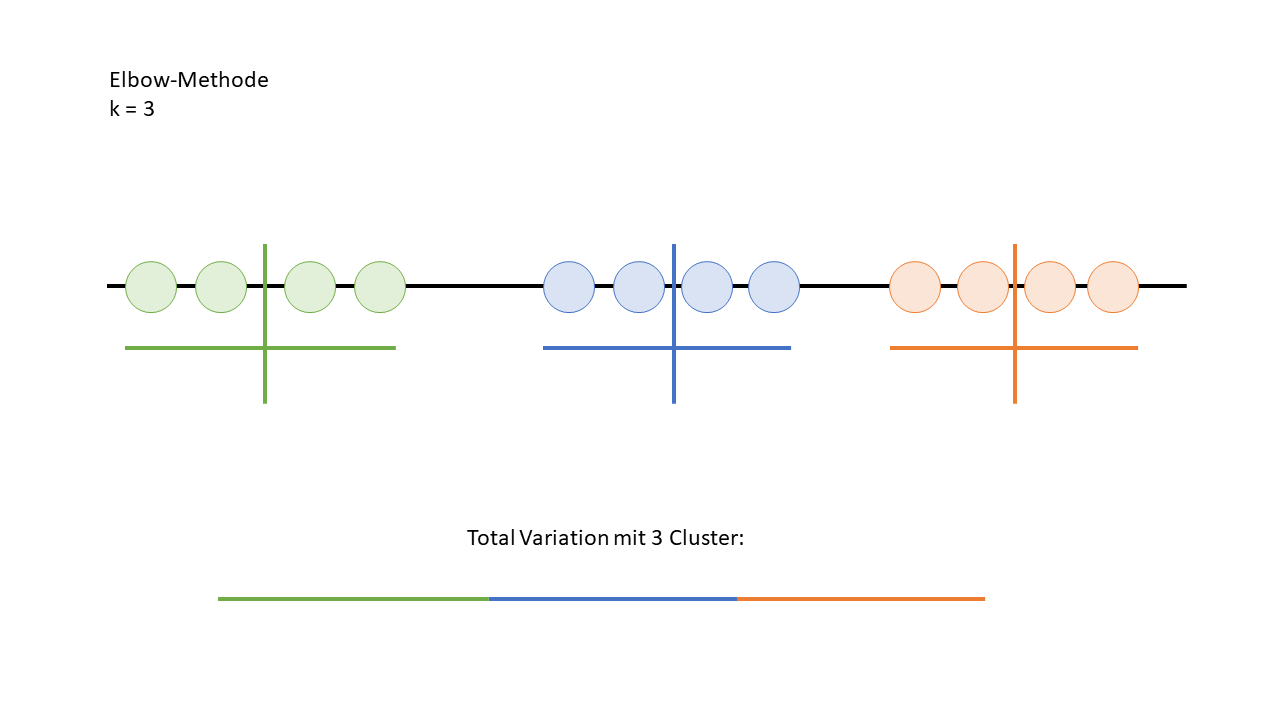
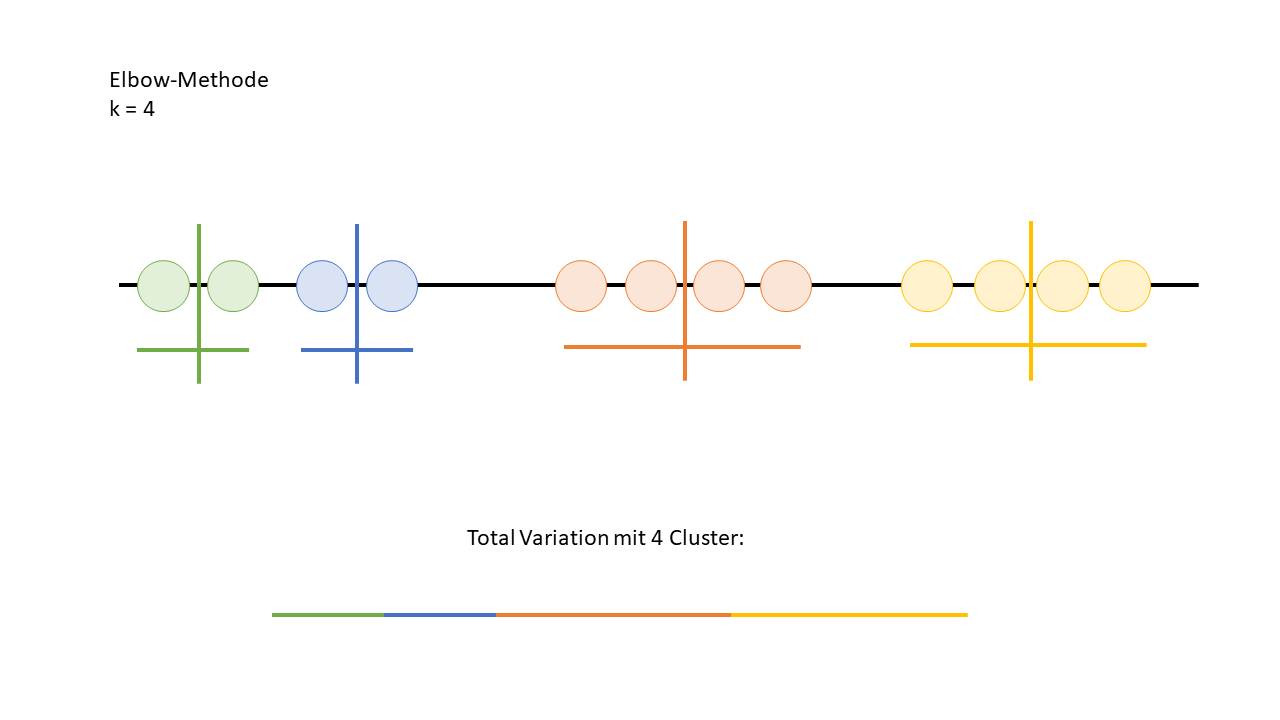
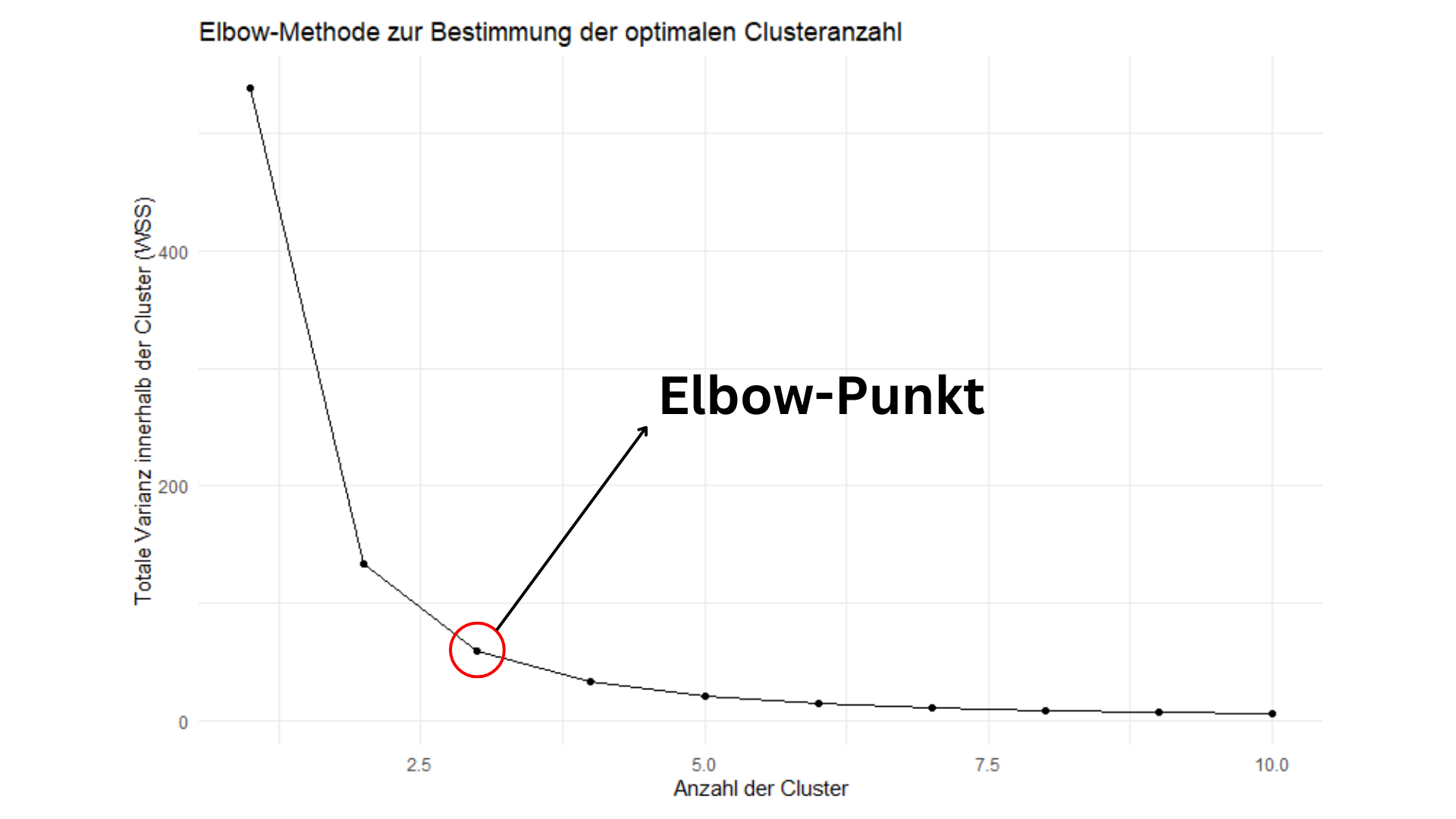
Wie man auf dem Bild sieht, verbessert sich die Variation ab vier Clustern nicht mehr signifikant. Das bedeutet, dass drei Cluster die optimale Anzahl sind. In der Praxis plottet man diese Werte normalerweise und erkennt den "Elbow-Punkt" direkt im Diagramm – also den Punkt, an dem die Kurve beginnt, flach zu verlaufen. Genau das ist auf dem unteren Bild zu sehen.
Der dazu gehörige R-Code:
artikel_umsatz <- artikel_umsatz %>%
arrange(desc(Umsatz_summe)) %>%
mutate(kumulative_summe = cumsum(Umsatz_summe),
kumulative_prozent = kumulative_summe / sum(Umsatz_summe) * 100)
artikel_umsatz <- artikel_umsatz[!artikel_umsatz$kumulative_prozent %in% boxplot.stats(artikel_umsatz$kumulative_prozent)$out, ]
set.seed(879823732)
wss <- sapply(1:10, function(k) {
kmeans(artikel_umsatz$kumulative_prozent, centers = k, nstart = 10000, iter.max = 10000)$tot.withinss
})
elbow_plot <- data.frame(
Cluster = 1:10,
WSS = wss
)
ggplot(elbow_plot, aes(x = Cluster, y = WSS)) +
geom_point() +
geom_line() +
labs(title = "Elbow-Methode zur Bestimmung der optimalen Clusteranzahl",
x = "Anzahl der Cluster",
y = "Totale Varianz innerhalb der Cluster (WSS)") +
theme_minimal()K-means Clusteranalyse bildlich aufgezeigt
Jetzt, da wir dank der Elbow-Methode wissen, dass 3 Cluster perfekt für unser Test-Dataset sind, können wir die Daten entsprechend aufteilen. In der einfachen ABC-Analyse haben wir das bereits gemacht, indem wir folgende Annahmen getroffen haben:
- Kumulativer Prozentsatz ≤ 20% = 3 Punkte
- Kumulativer Prozentsatz ≤ 50% = 2 Punkte
- Kumulativer Prozentsatz > 50% = 1 Punkt
Aber mal ehrlich, eigentlich macht es viel mehr Sinn, die Schwellenwerte für 20% und 50% datenbasiert zu berechnen. Woher sollen wir schliesslich wissen, dass nur Artikel mit einem kumulativen Prozentsatz unter 20% drei Punkte bekommen sollten? Genau hier kommt die K-means-Clusteranalyse ins Spiel.
Indem wir die Daten in Cluster aufteilen, können wir präzisere und fundiertere Schwellenwerte festlegen, anstatt uns auf starre Vorgaben zu verlassen. So stellen wir sicher, dass die Einteilung der Artikel auch wirklich den tatsächlichen Daten entspricht und nicht nur einer pauschalen Annahme folgt.
Erklärung K-means Clusteranalyse
Stell dir vor, wir nehmen all unsere Datenpunkte und platzieren sie entlang einer Linie, die von 0% bis 100% kumulativem Prozentsatz reicht. Dabei ist 0% kumulativ das Beste, also die "Top-Artikel" oder die besten Datenpunkte befinden sich ganz links auf dieser Linie.
Jetzt geht es darum, die Datenpunkte von Hand den verschiedenen Clustern zuzuordnen. Das heisst, wir schauen uns an, wo sich die Datenpunkte auf dieser Linie sammeln, und versuchen, sie nach Augenmass in Gruppen einzuteilen.
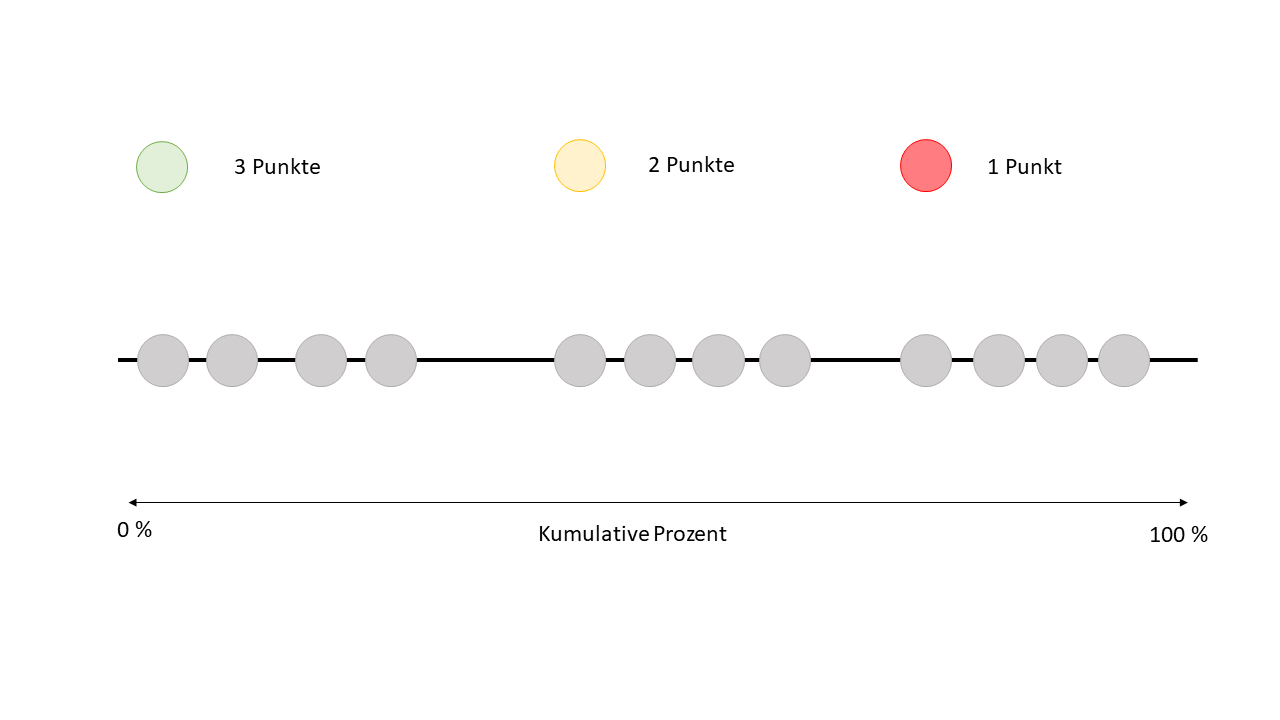
Auf dem unteren Bild siehst Du jetzt die optimale Zuordnung der Cluster und vermutlich hast Du gemerkt dass dies bei diesem Bild ziemlich einfach ist nach Augenmass.
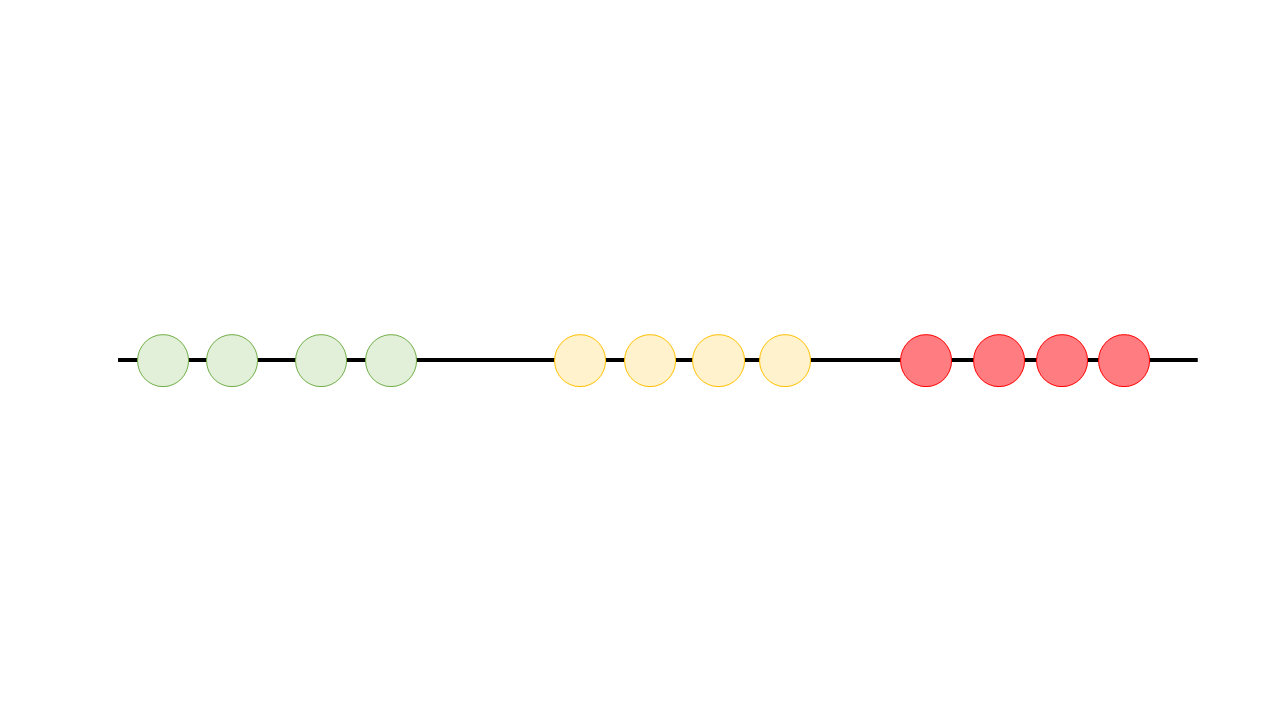
Schritt 1 / Clusteranzahl definieren
Für uns Menschen mag es einfach erscheinen, Datenpunkte nach Augenmass zu gruppieren, aber für einen Algorithmus ist das deutlich anspruchsvoller. Der erste Schritt besteht darin, dem Algorithmus mitzuteilen, in wie viele Cluster er die Daten aufteilen soll. In unserem Fall haben wir uns logischerweise für 3 Cluster entschieden.
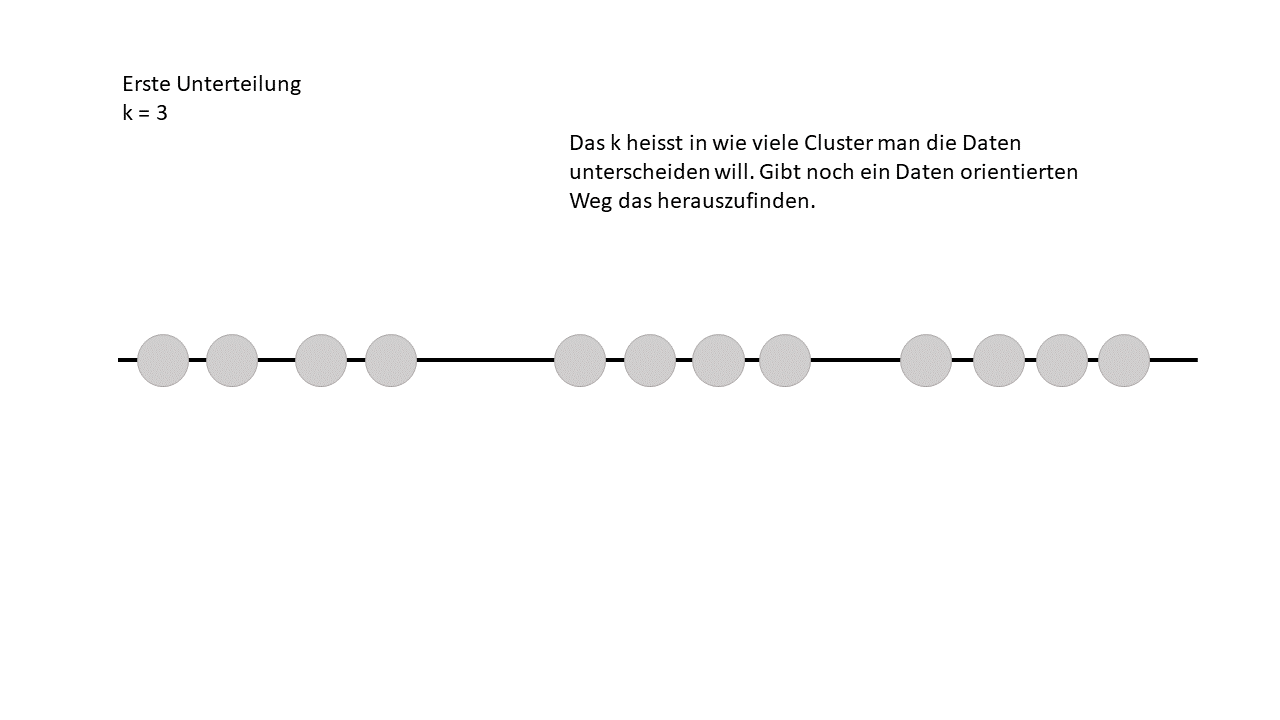
Schritt 2 / Clusterpunkte werden ausgewählt
Jetzt sucht sich der Algorithmus einfach drei Clusterpunkte aus – und das völlig zufällig. Er hat also keine Ahnung, wo die besten Stellen sind, sondern startet erstmal mit einem wilden Raten.
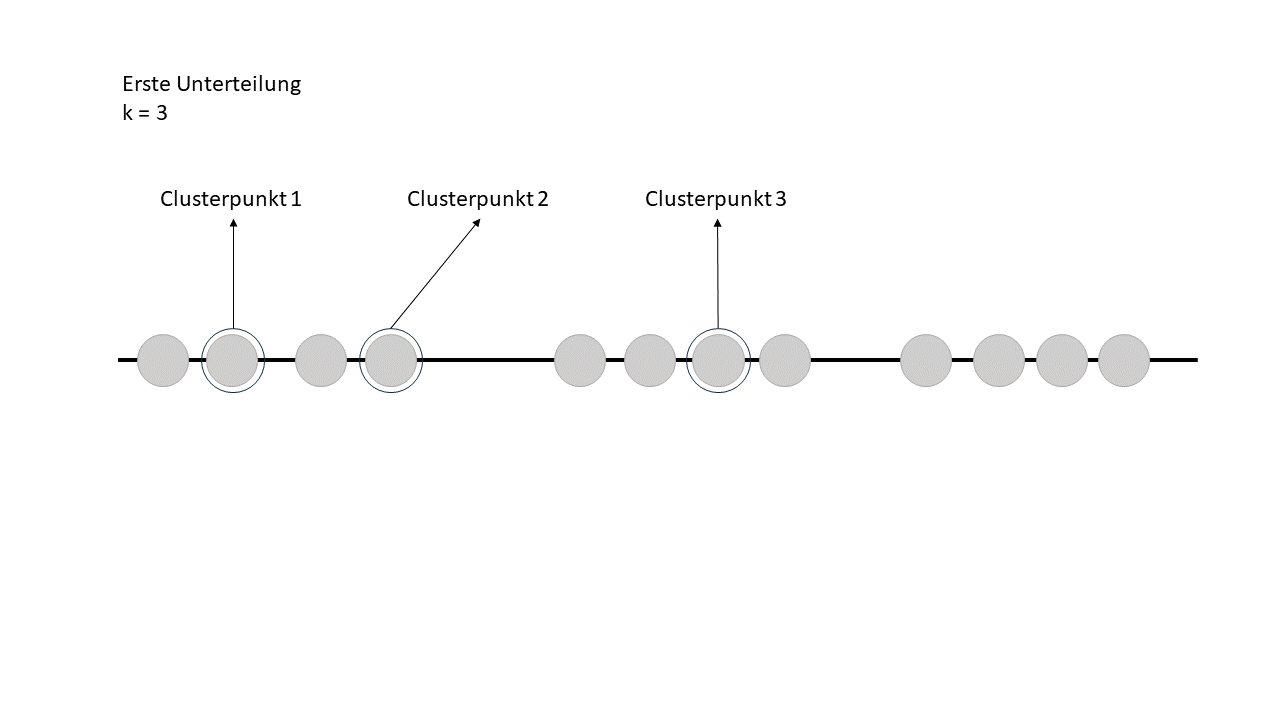
Schritt 3 / Distanz vom ersten Datenpunkt zu den Clusterpunkten
Im nächsten Schritt berechnet der Algorithmus die Distanz vom ersten Datenpunkt zu jedem der drei zufällig ausgewählten Clusterpunkte. Er schaut also, wie weit dieser Datenpunkt von jedem der Cluster entfernt ist, um dann zu entscheiden, zu welchem Cluster er am besten passt. Das Ganze läuft nach dem Prinzip „Wer ist mein nächster Nachbar?“ ab – der Datenpunkt wird dem Cluster zugeordnet, dessen Punkt ihm am nächsten liegt.
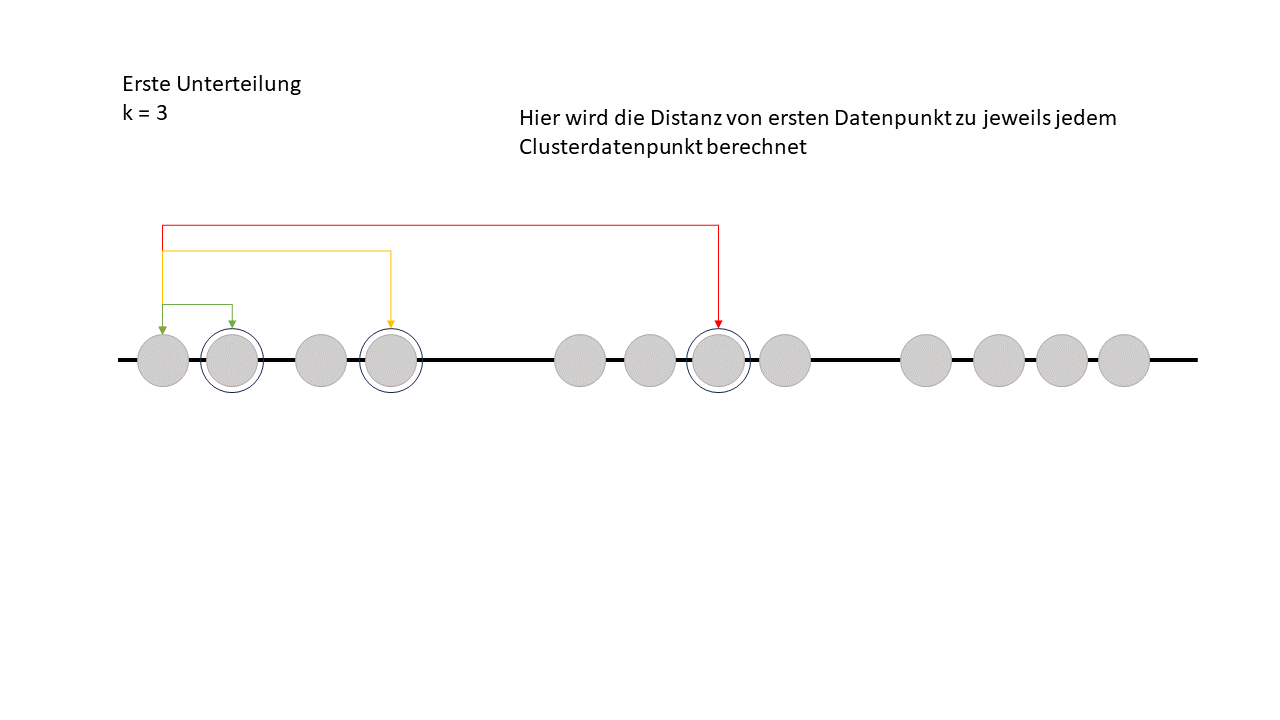

Nun geht der Algorithmus zum nächsten Datenpunkt welcher nicht als Cluster Punkt ausgewählt ist und macht dort nochmal dasselbe.
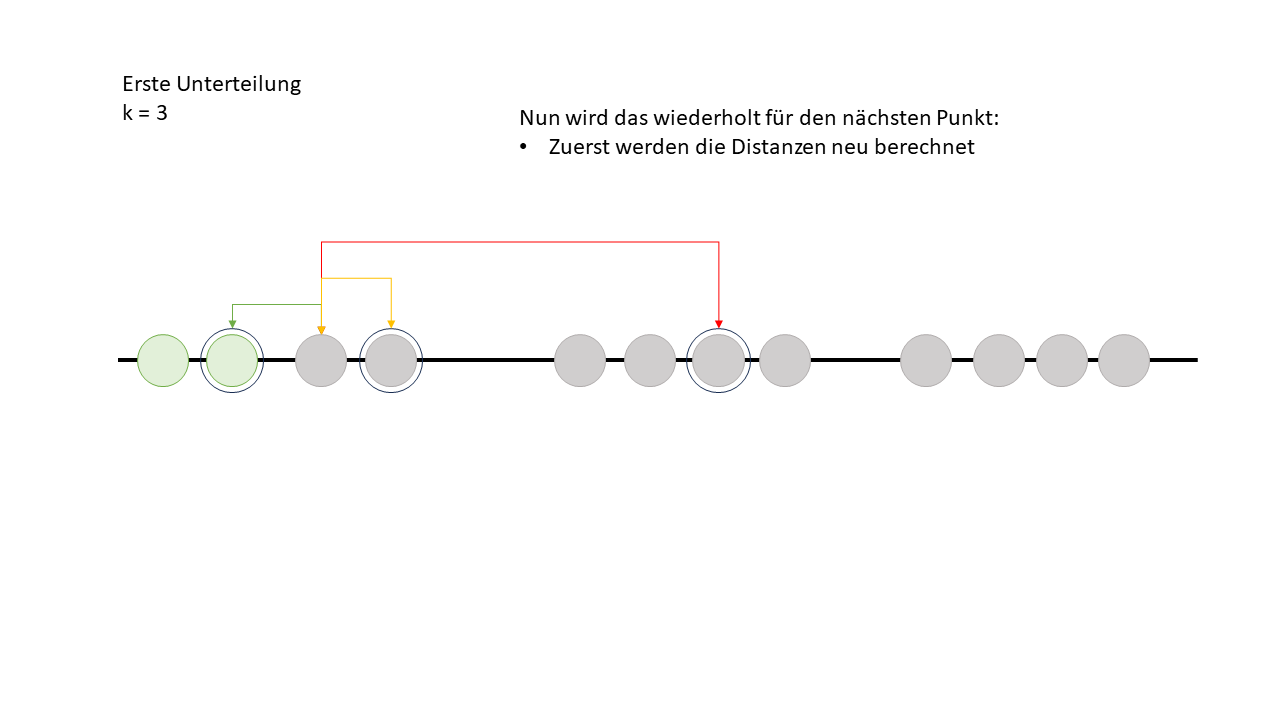


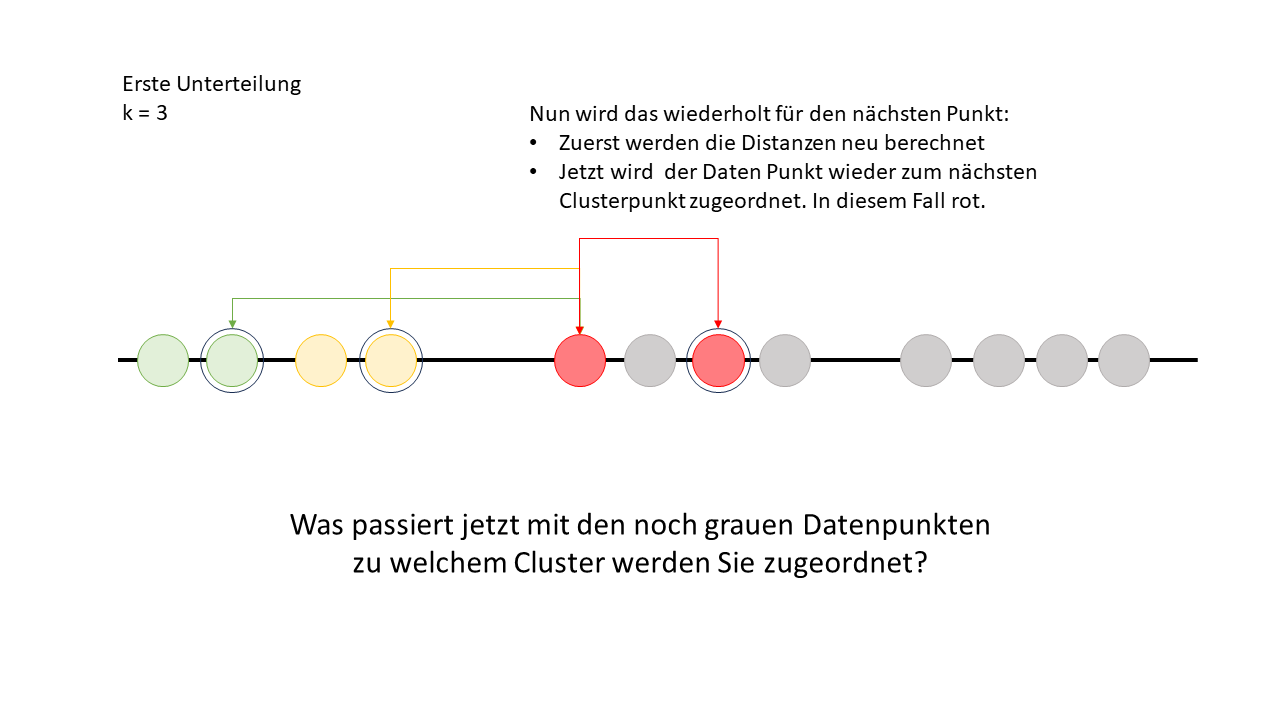
Um die Frage auf dem letzten Bild zu beantworten: Alle Datenpunkte werden dem roten Cluster zugeordnet, da die Distanz zu den anderen Clusterpunkten immer grösser wäre als zum roten. Das bedeutet, dass der rote Clusterpunkt der nächste Nachbar für alle Datenpunkte ist.
Als nächster Schritt wird dann der Durchschnitt jedes Clusters berechnet, was wir als den "Zentrumspunkt" oder das "Centroid" des Clusters bezeichnen. Aber keine Sorge, dieser Schritt hat im Moment noch keinen Einfluss auf unsere aktuelle Analyse. Warum das so ist und welche Rolle diese Durchschnittsberechnung später spielt, werden wir in einer späteren Analyse genauer betrachten.

Jetzt können wir die Varianz innerhalb der Cluster sichtbar machen, indem wir eine Linie unter jedem Cluster ziehen. Diese Linien führen wir dann zusammen, um die gesamte Variation vom ersten Cluster zu sehen. Das gibt uns einen Eindruck davon, wie stark die Datenpunkte innerhalb des Clusters streuen.
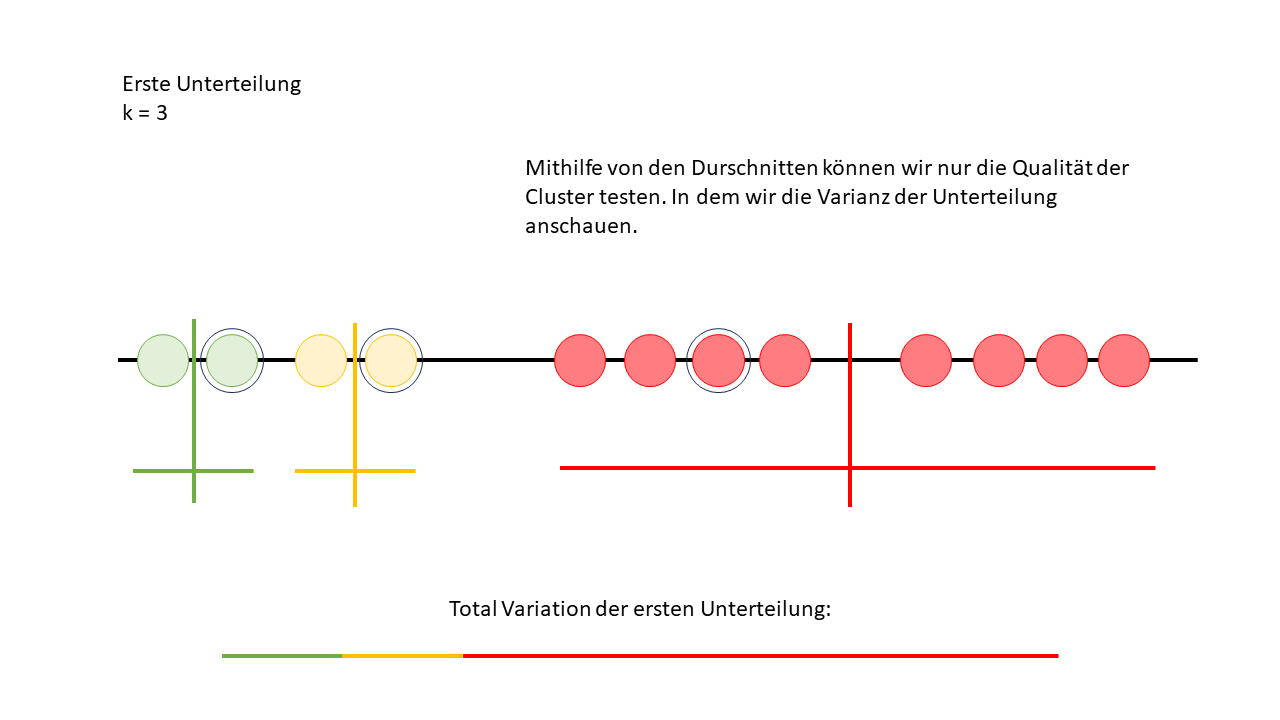
Wie man auf dem unteren Bild sehen kann, ist der Algorithmus nicht ganz so flink wie unser Auge und konnte im ersten Schritt den richtigen Cluster noch nicht direkt erkennen. Das zeigt, dass der Algorithmus noch etwas mehr Versuche braucht, während unser menschliches Auge oft intuitiv die richtige Gruppierung erkennt.
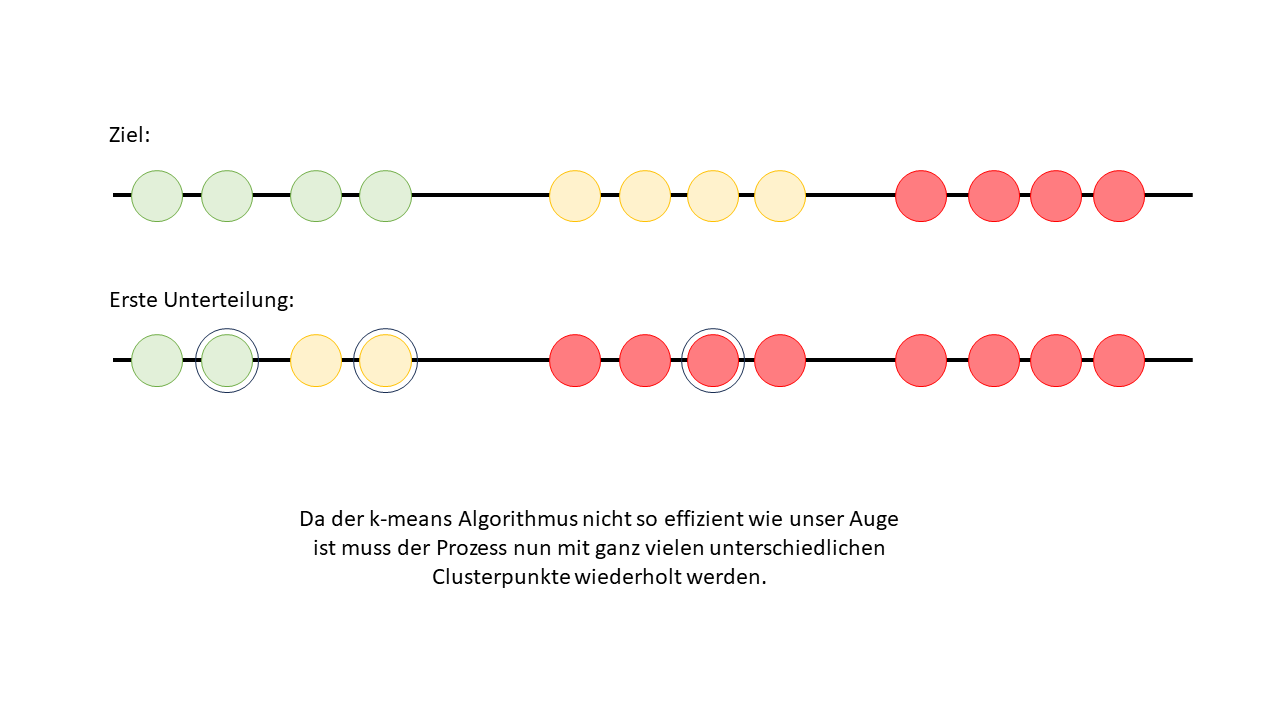
Wiederholung der drei Schritte
Deshalb startet der Algorithmus direkt einen zweiten Versuch wo er dann wieder zufällige Clusterpunkte setzt.

Anschliessend werden die Distanzen erneut berechnet, und die Datenpunkte werden wieder den Clustern zugeordnet. Danach wird erneut der Durchschnittswert jedes Clusters berechnet, um die Clusterzentren anzupassen. So nähert sich der Algorithmus Schritt für Schritt einer besseren Lösung an.
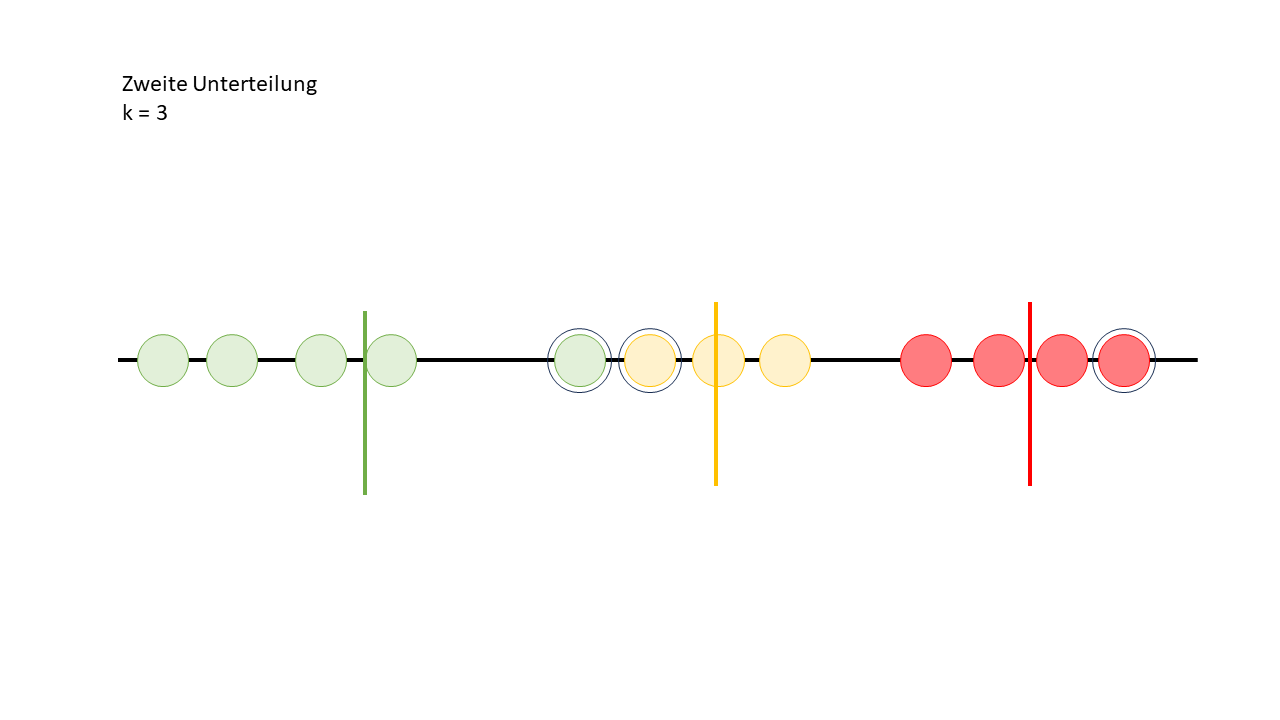
Jetzt wird es Zeit, die Erklärung nachzuholen, warum wir die Durchschnittswerte berechnen. Eigentlich passiert Folgendes: Nachdem die Durchschnittswerte der Clusterpunkte berechnet wurden, werden alle Datenpunkte nochmal zurückgesetzt und neu den Clustern zugeordnet – und zwar basierend auf diesen Durchschnittswerten. Diese Durchschnittswerte werden dann zu den neuen Clusterzentren. Das heisst, der Algorithmus verschiebt die Clusterzentren immer wieder, bis die Datenpunkte optimal gruppiert sind. So verfeinert sich die Zuordnung mit jedem Schritt.


Nun kann man sehen, dass sich nach der zweiten Zuordnung ein Datenpunkt zu einem anderen Cluster verschoben hat.
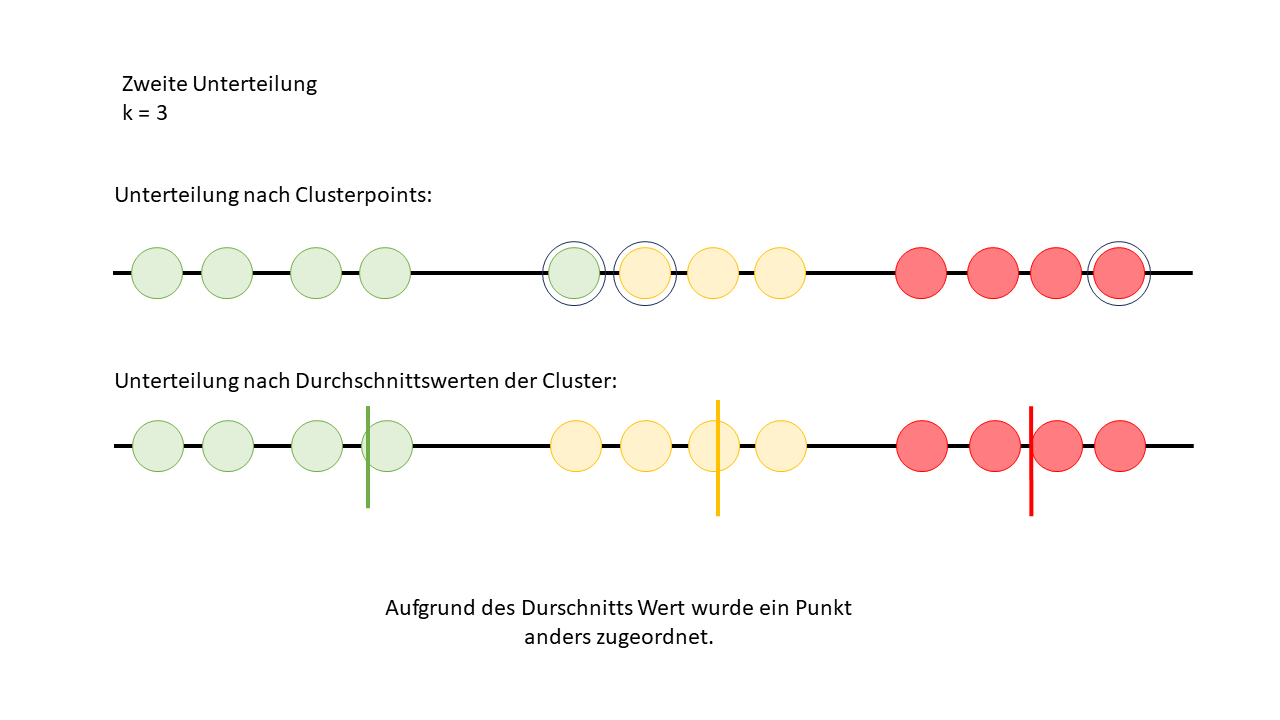
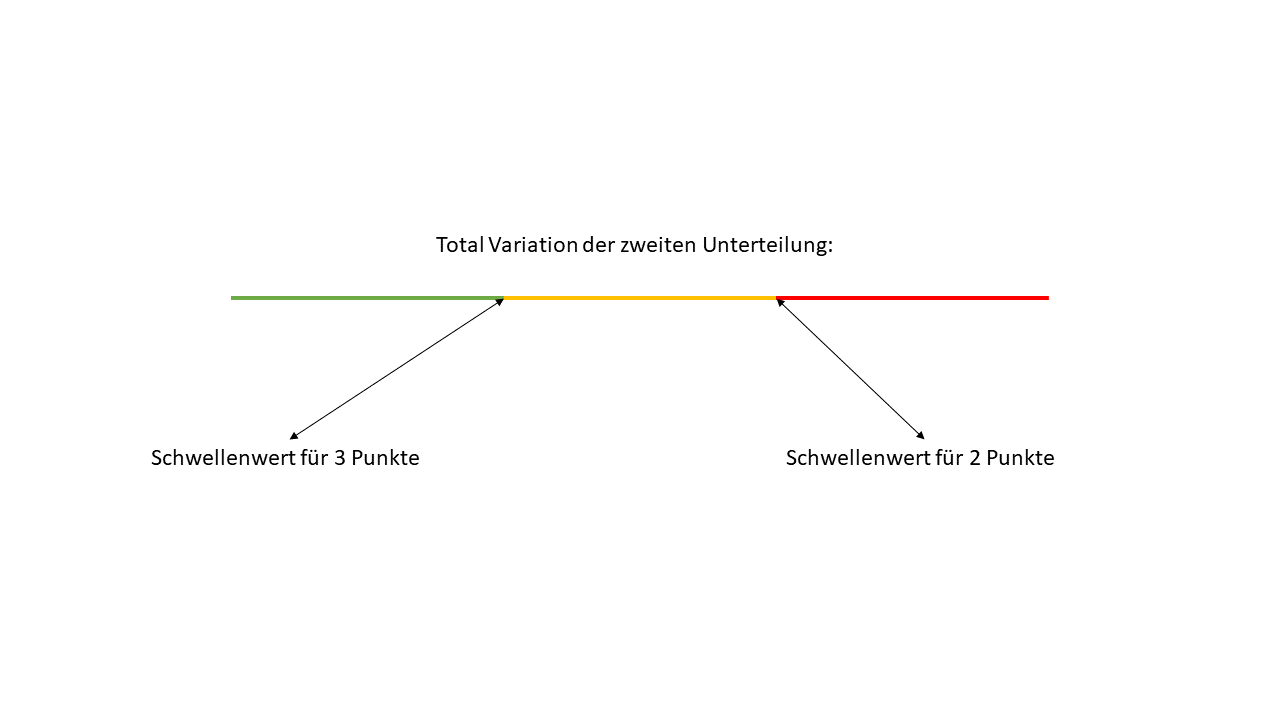
Jetzt haben wir eine weitere Gesamtvariation, und zwar von der zweiten Unterteilung der Daten. Als nächstes mache ich noch eine dritte Unterteilung, und dann nehmen wir an, dass ich von Anfang an nur drei Durchläufe geplant hatte. Das bedeutet, nach dem dritten Durchlauf stoppen wir den Algorithmus, auch wenn er theoretisch weiter optimieren könnte.
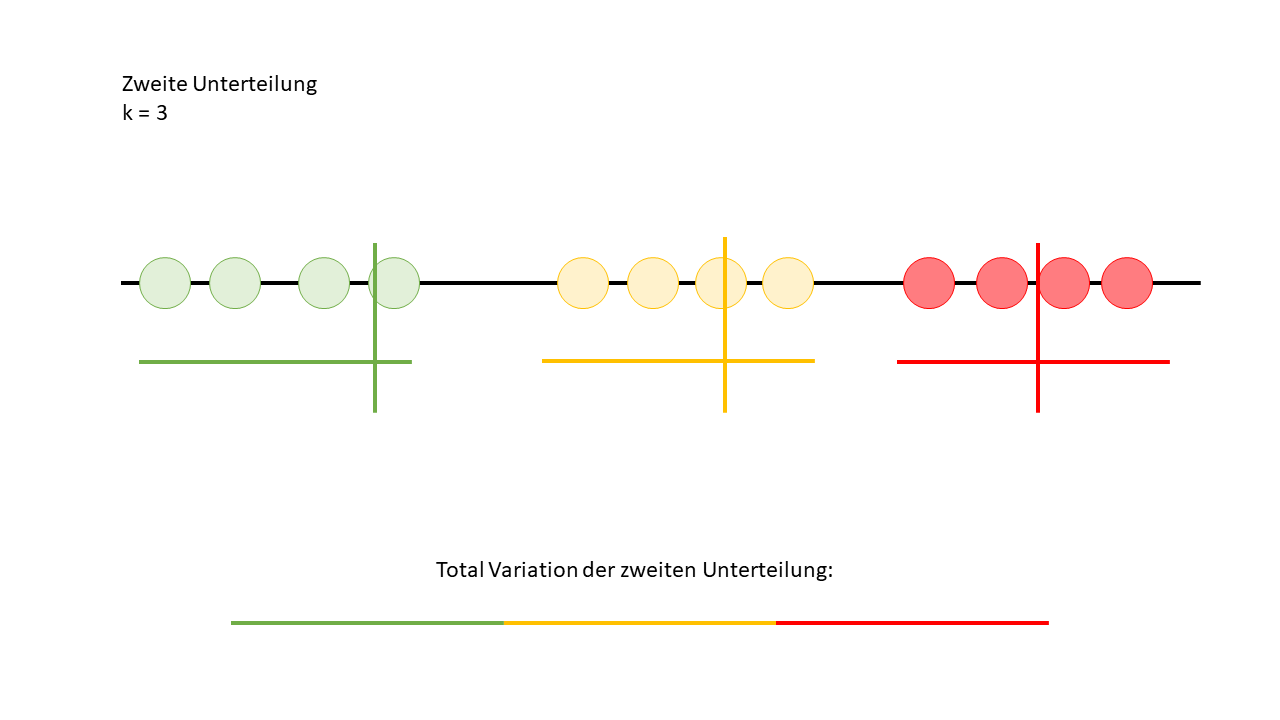

Bewertung der Gesamtvariationen
Jetzt können wir die drei Gesamtvariationen miteinander vergleichen, und der Algorithmus wählt die gleichmässigste Variation als "Gewinner" aus. Wenn wir dann diese Variation anschauen, können wir den höchsten Wert vom mittleren Cluster und den höchsten Wert vom hintersten Cluster nehmen und diese als Schwellenwerte nutzen, um festzulegen, wie die Punkte in einer ABC-Analyse vergeben werden sollten. So haben wir eine datengetriebene Methode, die uns präziser zeigt, welche Artikel oder Datenpunkte in welche Kategorie fallen.